经验误差与过拟合

错误率： 分类错误样本数占样本总数
精度： 1 - 错误率

误差：学习器事假预测输出样本与样本真实输出之间的差异

在训练集上的误差————“训练误差”（“经验误差”）
在新样本上的误差————“泛化误差”

我们希望泛化误差小，但是实际无法预知新样本只能采用“经验误差”最小化。

过拟合：把训练样本自身的一些特点当成所有潜在样本的“普遍规律”，导致泛化性能下降。
欠拟合：对训练样本的一般性质尚未学好。

模型选择问题：理想方案是对候选模型的泛化误差进行评估，选择最小的。但是无法直接获得泛化误差，而训练误差又容易导致过拟合。如何进行模型评估与选择？看下一节。

评估方法

以测试集来测试学习器对新样本的判别能力，以测试误差作为泛化误差的近似。通常假设测试样本也是从样本真实分布的独立同分布采样获得。
需要注意测试集应该尽可能与训练集互斥，即测试样本尽量不在训练集中出现、未在训练过程中使用过。
于是需要对数据D进行划分出训练集S和测试集T。

留出法

直接将数据集D划分为两个互斥的集合S和T。在S训练出模型，用T评估测试误差。
需要注意，训练/测试集应该尽可能保持数据的一致性，避免由于数据划分过程引入产生额外的偏差而对最终结果产生影响。

单次留出法往往结果不够准确，一般采用若干次随机划分、重复实验评估取平局值。但是S与T的取值一般是2/3~4/5用于S，剩余用于测试.

交叉验证

将D划分为k个大小相似的互斥子集（分层采样）。每次取k-1个子集做训练集，剩下1个做测试集，进行k次训练和测试，最终返回均值，也称作“k折交叉验证”。交叉验证的稳定和保真性取决于k，k一般取值为10，其他的有5,20等。

将数据进行划分通常要随机使用不同的划分p次，取p次k折交叉验证均值，如“10次10折交叉验证”。

若D包含m个样本，k=m称作“留一法”，该方法不收样本划分方式的影响。往往认为比较准确，但是数据集交大时候开销过大。另外NFL表明未必比其他评估算法准确。

自助法（bootstrapping）

减少样本S和T规模不同造成的影响。

具体步骤如下：

给定包含m个样本的数据集D，我们对他进行采样产生数据集D’:每次随机从D中挑选一个样本个样本，将其拷贝放到D’中，然后再将该样本重新放回初始数据集D，使得该样本在下次采样时候仍有可能被采到；这个过程重复m次以后就得到包含m个样本的D’。显然D中有一部分样本会在D‘中重复出现多次，而一些则不会出现，不会出现的概率是：
$$\lim_{m\to{\infty}} (1-\frac{1}{m} ) \to \frac{1}{e}\approx 0.368$$
即原始数据集中有36.8%不会出现在D’中。

于是我们可以用D’做训练集，D/D’做测试集，这样实际评估的模型与期望评估的模型都是用m个样本。而仍有1/3没在训练集中的样本用于测试。这样的测试结果称作“包外估计”。

优缺点

优点：

• 数据集较小，难以划分训练、测试集时很有用
• 能从原始数据集产生多个不同训练集，对集成学习等有很大好处
  缺点：
• 改变了原始数据集分布，会引入估计误差。
  因此，在初始数据量足够时，留出法和交叉验证使用更多。

调参与最终模型

由于大多数算法有参数设置，需要根据范围和步长进行实验，对模型进行评估。
模型评估中选做评估测试的数据集称为“验证集”。
例如，在研究对比不同算法的泛化性能时候，我们用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和测试集，基于验证集上的性能来进行模型选择和调参。（这样训练数据不会变少了？）

性能度量

回归任务中常用的度量是均分误差。
下面介绍分类任务中常用的性能度量。

错误率与精度

查准率、查全率与F1

对于二分类问题，可以根据真实类别与预测列别组合成下表：

真实情况	预测	结果
	正例	反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN（真反例）

查全率P（Precision）查准率R（Recall）如下：
$ P = \frac{TP}{TP+FP}$ (预测为正例的结果中真正例的比例)（包含反例预测为正例）
$ R = \frac{TP}{TP+FN}$ （所有正例中真正例的比例）（包含正例预测为反例）

查准率和查全率是一对矛盾的度量。

例如，希望尽可能多的好瓜被选出来，就加大选瓜数量，将所有西瓜都选上，这样好瓜数量也能增大，但是查准率就比较低；希望选出来瓜好瓜比率尽可能高，可以只挑选有把握的瓜，这样查全率就比较低。

我们可以根据学习器的预测结果对样例进行排序，排在前面的额事学习器认为“最可能是”正例的样本，排在后面的是“最不可能”是正例的样本。按此顺序逐个把样本进行预测，每次可以计算出当前的查全率、查准率。以Precision为纵轴，Recall为横轴可以画出“PR曲线”。

通常一个学习器PR曲线被另一个包围，认为后者优于前者。
但交叉的时候就难以断言。合理判断是根据PR下面积，但是面积难以判断
因此设计综合考虑度量：

平衡点（Break-Even Point, BEP）

查准率=查全率时的取值。

F1度量

$$F1 = \frac{2PR}{P+R} = \frac{2*TP}{样例总数+TP-TN}$$

更一般的$F_{\beta}$

$$F_{\beta} = \frac{(1+\beta^2)PR}{\beta^2 * P+R}$$

多次训练、测试产生多个混淆矩阵时

1. 宏查全率、宏查准率、宏F1
   分别计算Precision和 Recall，然后求平均再计算F1

2. 宏查全率、宏查准率、宏F1
   平均对应TP，FP…加起来平均，再计算F1

ROC与AUC

很多学习器是为测试样本产生一个实值或者概率预测，然后将预测值与分类阈值进行比较，若大于阈值判定为正，否则为反。这个实值决定了学习器泛化能力。
注意ROC与PR的不同
ROC纵轴是真正例率，横轴是假正例率。
$ TPR = \frac{TP}{TP+FN}$ (实际正例的结果中真正例的比例)
$ FPR = \frac{FP}{TN+FP}$ （实际反例中假正例的比例）

真实情况	预测	结果
	正例	反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN（真反例）

真正例率是所有真实正例中真正例的比例；
假正例率是所有真实反例中假正例的比例；
查准率是所有预测正例中真正例的比例；
查全率是所有真实正例中真正例的比例；
所以查全率与真正例率相等 ， R=TPR

通常一个学习器ROC曲线被另一个包围，认为后者优于前者。
但交叉的时候就难以断言。合理判断是根据ROC下面积–AUC。
形式化的看AUC考虑的是样本预测的排序质量，与排序误差有紧密联系。

排序损失 $\mathbf{l}_{rank}$

$$AUC = 1- \mathbf{l}_{rank}$$

PR与ROC

ROC与PR区别,分析来源
在ROC空间，ROC曲线越凸向左上方向效果越好。与ROC曲线左上凸不同的是，PR曲线是右上凸效果越好。

ROC和PR曲线都被用于评估机器学习算法对一个给定数据集的分类性能，每个数据集都包含固定数目的正样本和负样本。而ROC曲线和PR曲线之间有着很深的关系。

定理1：对于一个给定的包含正负样本的数据集，ROC空间和PR空间存在一一对应的关系，也就是说，如果recall不等于0，二者包含完全一致的混淆矩阵。我们可以将ROC曲线转化为PR曲线，反之亦然。

定理2：对于一个给定数目的正负样本数据集，一条曲线在ROC空间中比另一条曲线有优势，当且仅当第一条曲线在PR空间中也比第二条曲线有优势。（这里的“一条曲线比其他曲线有优势”是指其他曲线的所有部分与这条曲线重合或在这条曲线之下。）

证明过程见文章《The Relationship Between Precision-Recall and ROC Curves》

当正负样本差距不大的情况下，ROC和PR的趋势是差不多的，但是当负样本很多的时候，两者就截然不同了，ROC效果依然看似很好，但是PR上反映效果一般。解释起来也简单，假设就1个正例，100个负例，那么基本上TPR可能一直维持在100左右，然后突然降到0.如图，(a)(b)分别为正负样本1:1时的ROC曲线和PR曲线，二者比较接近。而(c)(d)的正负样本比例为1:1，这时ROC曲线效果依然很好，但是PR曲线则表现的比较差。这就说明PR曲线在正负样本比例悬殊较大时更能反映分类的性能。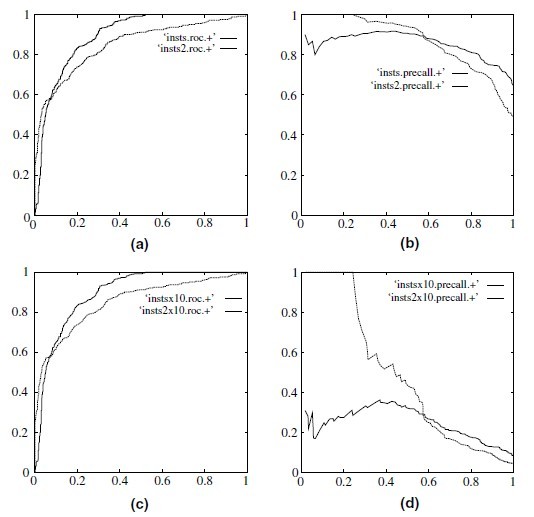

代价敏感错误率与代价曲线

根据任务的领域知识设定代价矩阵。（可以认为前面的度量默认各项代价均等）
对应的ROC曲线叫代价曲线。

比较检验

性能比较影响因素：1、泛化性能VS测试集性能 2、测试集选择 3、算法随机性。
采用统计假设检验推断学习器A泛化性能是否在统计意义上优于B，并且把握多大。

假设检验

下面的是针对单个学习器泛化性能的假设进行检验。

二项检验

一个测试错误率推测泛化错误率分布。

t检验

多个测试错误率。

针对多个学习器采用下文：

交叉验证t检验

McNemar检验

Fridman检验与Nemenyi检验

偏差与方差

“偏差方差分解”是解释学习算法泛化性能的重要工具，可以对期望泛化误差率进行拆解。
泛化误差可以分解为偏差、方差和噪声之和。