By

Contents
  1. 1. 问题来源
  2. 2. 应用场景
  3. 3. 简介
  4. 4. 算法原理
    1. 4.1. 环形空间
    2. 4.2. 把数据通过一定的hash算法处理后映射到环上
    3. 4.3. 将机器通过hash算法映射到环上
    4. 4.4. 机器的删除与添加
      1. 4.4.1. 1.节点（机器）的删除
      2. 4.4.2. 2.节点（机器）的添加
    5. 4.5. 平衡性
  5. 5. 附录：常用的hash算法
  6. 6. 代码实现
    1. 6.1. 简介
    2. 6.2. 实现类

来源：http://blog.csdn.net/cywosp/article/details/23397179/

问题来源

tencent2012笔试题附加题
问题描述： 例如手机朋友网有n个服务器，为了方便用户的访问会在服务器上缓存数据，因此用户每次访问的时候最好能保持同一台服务器。
已有的做法是根据ServerIPIndex[QQNUM%n]得到请求的服务器，这种方法很方便将用户分到不同的服务器上去。但是如果一台服务器死掉了，那么n就变为了n-1，那么ServerIPIndex[QQNUM%n]与ServerIPIndex[QQNUM%（n-1）]基本上都不一样了，所以大多数用户的请求都会转到其他服务器，这样会发生大量访问错误。

问： 如何改进或者换一种方法，使得：

(1) 一台服务器死掉后，不会造成大面积的访问错误，
(2)原有的访问基本还是停留在同一台服务器上；+
(3)尽量考虑负载均衡。（思路：往分布式一致哈希算法方面考虑。）

应用场景

在做服务器负载均衡时候可供选择的负载均衡的算法有很多，包括： 轮循算法（Round Robin）、哈希算法（HASH）、最少连接算法（Least Connection）、响应速度算法（Response Time）、加权法（Weighted ）等。其中哈希算法是最为常用的算法.
典型的应用场景是： 有N台服务器提供缓存服务，需要对服务器进行负载均衡，将请求平均分发到每台服务器上，每台机器负责1/N的服务。

常用的算法是对hash结果取余数 (hash() mod N)：对机器编号从0到N-1，按照自定义的hash()算法，对每个请求的hash()值按N取模，得到余数i，然后将请求分发到编号为i的机器。但这样的算法方法存在致命问题，如果某一台机器宕机，那么应该落在该机器的请求就无法得到正确的处理，这时需要将当掉的服务器从算法从去除，此时候会有(N-1)/N的服务器的缓存数据需要重新进行计算；如果新增一台机器，会有N /(N+1)的服务器的缓存数据需要进行重新计算。对于系统而言，这通常是不可接受的颠簸（因为这意味着大量缓存的失效或者数据需要转移）。

那么，如何设计一个负载均衡策略，使得受到影响的请求尽可能的少呢？
在Memcached、Key-Value Store、Bittorrent DHT、LVS中都采用了Consistent Hashing算法，可以说Consistent Hashing 是分布式系统负载均衡的首选算法。

简介

一致性哈希算法在1997年由麻省理工学院提出的一种分布式哈希（DHT）实现算法，设计目标是为了解决因特网中的热点(Hot spot)问题，初衷和CARP十分类似。一致性哈希修正了CARP使用的简 单哈希算法带来的问题，使得分布式哈希（DHT）可以在P2P环境中真正得到应用。
一致性hash算法提出了在动态变化的Cache环境中，判定哈希算法好坏的四个定义：

1. 平衡性(Balance)：平衡性是指哈希的结果能够尽可能分布到所有的缓冲中去，这样可以使得所有的缓冲空间都得到利用。很多哈希算法都能够满足这一条件。

2. 单调性(Monotonicity)：单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中，又有新的缓冲加入到系统中。哈希的结果应能够保证原有已分配的内容可以被映射到原有的或者新的缓冲中去，而不会被映射到旧的缓冲集合中的其他缓冲区。 

3. 分散性(Spread)：在分布式环境中，终端有可能看不到所有的缓冲，而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时，由于不同终端所见的缓冲范围有可能不同，从而导致哈希的结果不一致，最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的，因为它导致相同内容被存储到不同缓冲中去，降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生，也就是尽量降低分散性。 

4. 负载(Load)：负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中，那么对于一个特定的缓冲区而言，也可能被不同的用户映射为不同 的内容。与分散性一样，这种情况也是应当避免的，因此好的哈希算法应能够尽量降低缓冲的负荷。

算法原理

分布式集群中，对机器的添加删除，或者机器故障后自动脱离集群这些操作是分布式集群管理最基本的功能。如果采用常用的hash(object)%N算法，那么在有机器添加或者删除后，很多原有的数据就无法找到了，这样严重的违反了单调性原则。接下来主要讲解一下一致性哈希算法是如何设计的：

环形空间

按照常用的hash算法来将对应的key哈希到一个具有2^32次方个桶的空间中，即0~(2^32)-1的数字空间中。现在我们可以将这些数字头尾相连，想象成一个闭合的环形。如下图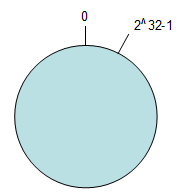

把数据通过一定的hash算法处理后映射到环上

现在我们将object1、object2、object3、object4四个对象通过特定的哈希函数计算出响应的key值，然后散列到Hash环上
Hash(Object1) = key1
Hash(Object2) = key2
Hash(Object3) = key3
Hash(Object4) = key4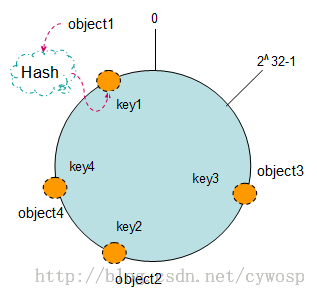

将机器通过hash算法映射到环上

在采用一致性哈希算法的分布式集群中将新的机器加入，其原理是通过使用与对象储存一样的hash算法将机器也映射到环中（一般情况下对机器的hash计算是采用机器的IP或者机器唯一的别名作为输入值），然后以顺时针方向计算，将所有的对象存储到离自己最近的机器中。
假设现在有NODE1，NODE2，NODE3三台机器，通过Hash算法得到对应的KEY值，映射到环中，其示意图如下：
Hash(NODE1) = KEY1;
Hash(NODE2) = KEY2;
Hash(NODE3) = KEY3;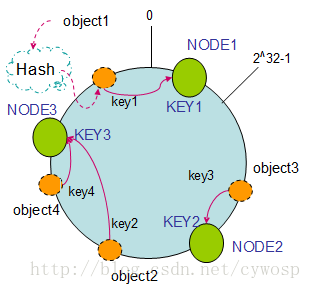

通过上图可以看出对象与机器处于同一哈希空间中，这样按顺时针转动object1存储到了NODE1中，object3存储到了NODE2中，object2、object4存储到了NODE3中。在这样的部署环境中，hash环是不会变更的，因此，通过算出对象的hash值就能快速的定位到对应的机器中，这样就能找到对象真正的存储位置了。

机器的删除与添加

普通hash求余算法最为不妥的地方就是在有机器的添加或者删除之后会照成大量的对象存储位置失效，这样就大大的不满足单调性了。下面来分析一下一致性哈希算法是如何处理的。

1.节点（机器）的删除

以上面的分布为例，如果NODE2出现故障被删除了，那么按照顺时针迁移的方法，object3将会被迁移到NODE3中，这样仅仅是object3的映射位置发生了变化，其它的对象没有任何的改动。如下图：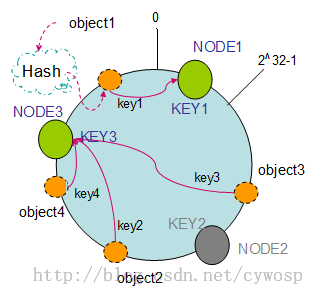

2.节点（机器）的添加

如果往集群中添加一个新的节点NODE4，通过对应的哈希算法得到KEY4，并映射到环中，如下图：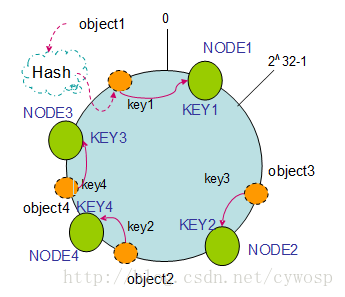

通过按顺时针迁移的规则，那么object2被迁移到了NODE4中，其它对象还保持这原有的存储位置。通过对节点的添加和删除的分析，一致性哈希算法在保持了单调性的同时，还是数据的迁移达到了最小，这样的算法对分布式集群来说是非常合适的，避免了大量数据迁移，减小了服务器的的压力。

平衡性

根据上面的图解分析，一致性哈希算法满足了单调性和负载均衡的特性以及一般hash算法的分散性，但这还并不能当做其被广泛应用的原由，因为还缺少了平衡性。下面将分析一致性哈希算法是如何满足平衡性的。hash算法是不保证平衡的，如上面只部署了NODE1和NODE3的情况（NODE2被删除的图），object1存储到了NODE1中，而object2、object3、object4都存储到了NODE3中，这样就照成了非常不平衡的状态。

在一致性哈希算法中，为了尽可能的满足平衡性，其引入了虚拟节点。

“虚拟节点”（ virtual node ）是实际节点（机器）在 hash 空间的复制品（ replica ）。
实际个节点（机器）对应了若干个“虚拟节点”，这个对应个数也成为“复制个数”，“虚拟节点”在 hash 空间中以hash值排列。

以上面只部署了NODE1和NODE3的情况（NODE2被删除的图）为例，之前的对象在机器上的分布很不均衡，现在我们以2个副本（复制个数）为例，这样整个hash环中就存在了4个虚拟节点，最后对象映射的关系图如下：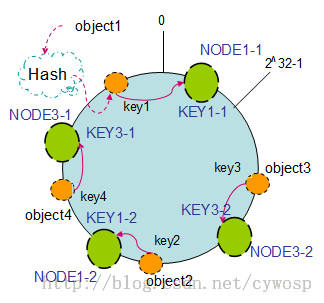

根据上图可知对象的映射关系：object1->NODE1-1，object2->NODE1-2，object3->NODE3-2，object4->NODE3-1。通过虚拟节点的引入，对象的分布就比较均衡了。那么在实际操作中，正真的对象查询是如何工作的呢？对象从hash到虚拟节点到实际节点的转换如下图：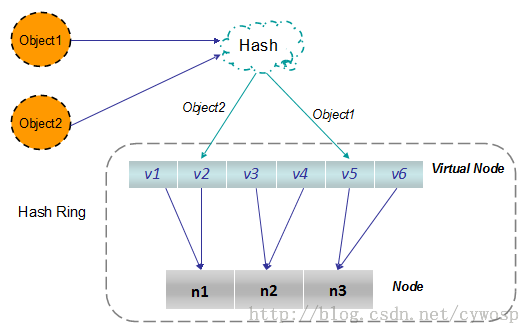

“虚拟节点”的hash计算可以采用对应节点的IP地址加数字后缀的方式。例如假设NODE1的IP地址为192.168.1.100。引入“虚拟节点”前，计算 cache A 的 hash 值：
Hash(“192.168.1.100”);
引入“虚拟节点”后，计算“虚拟节”点NODE1-1和NODE1-2的hash值：
Hash(“192.168.1.100#1”); // NODE1-1
Hash(“192.168.1.100#2”); // NODE1-2

附录：常用的hash算法

代码实现

来源：http://sgq0085.iteye.com/blog/2230528
http://www.blogjava.net/hello-yun/archive/2012/10/10/389289.html

简介

MurmurHash算法：高运算性能，低碰撞率，由Austin Appleby创建于2008年，现已应用到Hadoop、libstdc++、nginx、libmemcached等开源系统。2011年Appleby被Google雇佣，随后Google推出其变种的CityHash算法。官方只提供了C语言的实现版本。
Java界中Redis，Memcached，Cassandra，HBase，Lucene都用它。
在Java的实现，Guava的Hashing类里有，上面提到的Jedis，Cassandra里都有Util类。
但存在的问题是由于Java的数据类型long与C语言中无符号长整型uint64_t有区别，导致Java输出版本存在负数，针对这个问题进行了修改；另外需要注意的是中文不同编码（UTF-8或GBK）会导致输出结果的不同，使用中需要统一编码。

实现类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
public class Shard<S> { // S类封装了机器节点的信息 ，如name、password、ip、port等   
  
    private TreeMap<Long, S> nodes; // 虚拟节点   
    private List<S> shards; // 真实机器节点   
    private final int NODE_NUM = 100; // 每个机器节点关联的虚拟节点个数   
  
    public Shard(List<S> shards) {  
        super();  
        this.shards = shards;  
        init();  
    }  
  
    private void init() { // 初始化一致性hash环   
        nodes = new TreeMap<Long, S>();  
        for (int i = 0; i != shards.size(); ++i) { // 每个真实机器节点都需要关联虚拟节点   
            final S shardInfo = shards.get(i);  
  
            for (int n = 0; n < NODE_NUM; n++)  
                // 一个真实机器节点关联NODE_NUM个虚拟节点   
                nodes.put(hash("SHARD-" + i + "-NODE-" + n), shardInfo);  
  
        }  
    }  
  
    public S getShardInfo(String key) {  
        SortedMap<Long, S> tail = nodes.tailMap(hash(key)); // 沿环的顺时针找到一个虚拟节点   
        if (tail.size() == 0) {  
            return nodes.get(nodes.firstKey());  
        }  
        return tail.get(tail.firstKey()); // 返回该虚拟节点对应的真实机器节点的信息   
    }  
  
    /** 
     *  MurMurHash算法，是非加密HASH算法，性能很高， 
     *  比传统的CRC32,MD5，SHA-1（这两个算法都是加密HASH算法，复杂度本身就很高，带来的性能上的损害也不可避免） 
     *  等HASH算法要快很多，而且据说这个算法的碰撞率很低. 
     *  http://murmurhash.googlepages.com/ 
     */  
    private Long hash(String key) {  
          
        ByteBuffer buf = ByteBuffer.wrap(key.getBytes());  
        int seed = 0x1234ABCD;  
          
        ByteOrder byteOrder = buf.order();  
        buf.order(ByteOrder.LITTLE_ENDIAN);  
  
        long m = 0xc6a4a7935bd1e995L;  
        int r = 47;  
  
        long h = seed ^ (buf.remaining() * m);  
  
        long k;  
        while (buf.remaining() >= 8) {  
            k = buf.getLong();  
  
            k *= m;  
            k ^= k >>> r;  
            k *= m;  
  
            h ^= k;  
            h *= m;  
        }  
  
        if (buf.remaining() > 0) {  
            ByteBuffer finish = ByteBuffer.allocate(8).order(  
                    ByteOrder.LITTLE_ENDIAN);  
            // for big-endian version, do this first:   
            // finish.position(8-buf.remaining());   
            finish.put(buf).rewind();  
            h ^= finish.getLong();  
            h *= m;  
        }  
  
        h ^= h >>> r;  
        h *= m;  
        h ^= h >>> r;  
  
        buf.order(byteOrder);  
        return h;  
    }  
  
}
Contents
  1. 1. 问题来源
  2. 2. 应用场景
  3. 3. 简介
  4. 4. 算法原理
    1. 4.1. 环形空间
    2. 4.2. 把数据通过一定的hash算法处理后映射到环上
    3. 4.3. 将机器通过hash算法映射到环上
    4. 4.4. 机器的删除与添加
      1. 4.4.1. 1.节点（机器）的删除
      2. 4.4.2. 2.节点（机器）的添加
    5. 4.5. 平衡性
  5. 5. 附录：常用的hash算法
  6. 6. 代码实现
    1. 6.1. 简介
    2. 6.2. 实现类