Contents

1. k近邻模型
2. k近邻算法的实现：kd树

k-NN是一种基本的分类和回归方法。k近邻法的输入是实例的特征向量，对应于特征空间的点；输出是实例的类别，可以取多类。k近邻法假设给定一个训练数据集，其中的实例类别已定。分类是对于新的类别，根据其k个最近邻的训练实例的类别，通过多数表决法等方式进行预测。因此k近邻法不具有显性的学习过程，k近邻法实际上利用训练数据集对特征空间进行划分，并作为其分类的模型。

k值的选择、距离度量以及分类决策规则是k近邻的三个基本要素。

k近邻模型

距离度量

最常用的“闵可夫斯基距离”:
$$dist = {(\sum\limits_{k = 1}^n {|{p_k} - {q_k}{|^r}} )^{\frac{1}{r}}}$$

r = 2 , 即欧式距离
r = 1 , 即曼哈顿距离
r = $\infty $ ，即切比雪夫距离，各个坐标距离的最大值

由不同的距离度量确定的最近邻点是不同的

k值的选择

k值的选择会对k近邻算法产生重大影响。

如果k较小，学些的近似误差会减小，只有输入与实例较近的训练实例才会对决策结果起作用。缺点是预测结果会对近邻的实例点十分敏感，如果近邻的实例点恰好是噪音预测就会出错。
k小意味着模型变复杂，容易过拟合。

k较大，可以减少学习的估计误差，但是近似误差会增大。模型变简单。

k=N，简单预测实例在训练集中最多的类。

一般k取一个较小的值，通常用交叉验证法来选取。

分类决策规则

往往是多数表决。多数表决的规则等价于经验风险最小化。

k近邻算法的实现：kd树

k近邻算法最简单的实现是线性扫描，但是训练集很大的时候十分耗时。
为了提高k近邻搜索效率，考虑用特殊的结构存储训练数据，减少计算距离的次数。

构造kd树

kd树是一种对k为空间中的实例进行存储以便对齐进行快速检索的属性数据结构。kd树是二叉树，表示对k为空间的一个划分。构造kd树相当于不断地垂直于坐标轴的超平面将k为空间划分。构成一系列的k为超矩形区域。kd树的每个节点对应于一个k维超矩形区域。

构造kd树的方法：
构造根节点，使根节点对应于k维空间中包含所有实例点的超矩形区域；
通过下面的递归方法，不断的对k为空间进行切分，生成子节点。
在超矩形区域（结点）上选择一个坐标轴和此坐标轴上的一个且分点，确定一个超平面，这个超平面通过选定的且分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域（子结点）；这时，实例被分到两个子区域，这个过程知道区域内没有实例时终止（终止时的结点是叶节点）。在此过程，将实例保存在响应的结点上。

通常情况下。依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数为且分点，这样得到的kd树是平衡的。（平衡的kd树搜索效率未必最优）

构造平衡kd树的算法：

下面给出构造kd树的数据结构：

域名	数据类型	描述
Node-data	数据矢量	数据集中某个数据点，是k位矢量
Range	空间矢量	该点所表示的空间范围
split	整数	垂直于分割超平面的方向轴序号
left	kd树	左子树
right	kd树	右子树

从上面对k-d树节点的数据类型的描述可以看出构建k-d树是一个逐级展开的递归过程。下面给出的是构建k-d树的伪码。

算法：构建k-d树（createKDTree）  
输入：数据点集Dataset和其所在的空间Range  
输出：Kd，类型为k-d tree  
1.If Data-set为空，则返回空的k-d tree  
2.调用节点生成程序：  
　　（1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。假设每条数据记录为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；  
　　（2）确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Dataset = Dataset / Node-data（除去其中Node-data这一点）。  
3.dataleft = {d属于Dataset && d[split] ≤ Node-data[split]}  
   Left_Range = {Range && dataleft}  
  dataright = {d属于Dataset && d[split] > Node-data[split]}  
   Right_Range = {Range && dataright}  
4.left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_Range）。并设置left的parent域为Kd；  
   right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataleft，Left_Range）。并设置right的parent域为Kd。

以上述举的实例来看，过程如下：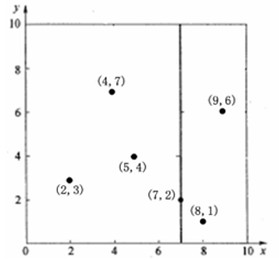

由于此例简单，数据维度只有2维，所以可以简单地给x，y两个方向轴编号为0,1，也即split={0,1}。

（1）确定split域的首先该取的值。分别计算x，y方向上数据的方差得知x方向上的方差最大，所以split域值首先取0，也就是x轴方向；

（2）确定Node-data的域值。根据x轴方向的值2,5,9,4,8,7排序选出中值为7，所以Node-data = （7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于split = 0（x轴）的直线x = 7；

（3）确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分，如下图所示。x <= 7的部分为左子空间，包含3个节点{（2,3），（5,4），（4,7）}；另一部分为右子空间，包含2个节点{（9,6），（8,1）}。

如算法所述，k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点（5,4）和（9,6）（也就是左右子空间的’根’节点），同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点，如下图所示。最后生成的k-d树如下图所示。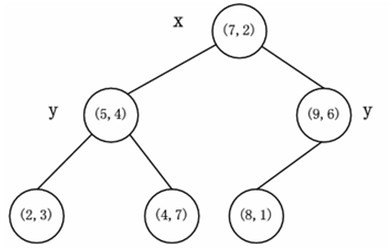

对于n个实例的k维数据来说，建立kd-tree的时间复杂度为O(k n logn)。

搜索kd树

下面叙述用kd树的最近邻搜索算法，KNN的类似：

在kd树中找出包含目标点x的叶节点：从根节点出发，递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子点，否咋移动到右子点，直到子节点为叶节点为止。
以此叶节点为“当前最近点”
递归的向上回退，在每个节点进行如下操作：
a. 如果该节点保存的实例点比当前最近点距离目标点更近，则以当前点为“当前最近点”
b. 当前最近点一定存在于该节点一个子节点对应的区域，检查该子节点的父节点的另一子节点对应的区域知否有更近的点。具体的，检查另一子节点对应的区域是否以目标点为球心、以目标点与“当前最近点”的距离为半径的超球体相交。
如果相交，可能在另一个子节点对应的区域neutral存在距目标点更近的点，移动到另一个子节点，接着，递归的进行最近邻搜索。
若不相交，向上回退。
当回退到根节点的时候，搜索结束，最后的“当前最近点”即为x的最近邻点。

如若数据随机分布，kd树搜索平均复杂度O(logN)，N是训练实例树。
kd树更适用于训练实例数远大于空间维度数时的k近邻搜索

在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。这里先以一个简单的实例来描述最邻近查找的基本思路。

星号表示要查询的点（2.1,3.1）。通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点（2,3）。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行’回溯’操作：算法沿搜索路径反向查找是否有距离查询点更近的数据点。此例中先从（7,2）点开始进行二叉查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的节点为小于（7,2）和（5,4），大于（2,3），首先以（2,3）作为当前最近邻点，计算其到查询点（2.1,3.1）的距离为0.1414，然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如下图所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）节点右子空间中去搜索。

再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。

一个复杂点了例子如查找点为（2，4.5）。同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<（7,2），（5,4），（4,7）>，取（4,7）为当前最近邻点，计算其与目标查找点的距离为3.202。然后回溯到（5,4），计算其与查找点之间的距离为3.041。以（2，4.5）为圆心，以3.041为半径作圆，如下图左所示。可见该圆和y = 4超平面交割，所以需要进入（5,4）左子空间进行查找。此时需将（2,3）节点加入搜索路径中得<（7,2），（2,3）>。回溯至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2，3），最近距离更新为1.5。回溯至（7,2），以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割，如下图右所示。至此，搜索路径回溯完。返回最近邻点（2,3），最近距离1.5。

法：k-d树最邻近查找  
输入：Kd，    //k-d tree类型  
     target  //查询数据点  
输出：nearest， //最邻近数据点  
     dist      //最邻近数据点和查询点间的距离  
1. If Kd为NULL，则设dist为infinite并返回  
2. //进行二叉查找，生成搜索路径  
   Kd_point = &Kd；                   //Kd-point中保存k-d tree根节点地址  
   nearest = Kd_point -> Node-data；  //初始化最近邻点  
   while（Kd_point）  
   　　push（Kd_point）到search_path中； //search_path是一个堆栈结构，存储着搜索路径节点指针  
 /*** If Dist（nearest，target） > Dist（Kd_point -> Node-data，target） 
   　　　　nearest  = Kd_point -> Node-data；    //更新最近邻点 
   　　　　Max_dist = Dist(Kd_point，target）；  //更新最近邻点与查询点间的距离  ***/  
   　　s = Kd_point -> split；                       //确定待分割的方向  
   　　If target[s] <= Kd_point -> Node-data[s]     //进行二叉查找  
   　　　　Kd_point = Kd_point -> left；  
   　　else  
   　　　　Kd_point = Kd_point ->right；  
   nearest = search_path中最后一个叶子节点； //注意：二叉搜索时不比计算选择搜索路径中的最邻近点，这部分已被注释  
   Max_dist = Dist（nearest，target）；    //直接取最后叶子节点作为回溯前的初始最近邻点  
  
3. //回溯查找  
   while（search_path != NULL）  
   　　back_point = 从search_path取出一个节点指针；   //从search_path堆栈弹栈  
   　　s = back_point -> split；                   //确定分割方向  
   　　If Dist（target[s]，back_point -> Node-data[s]） < Max_dist   //判断还需进入的子空间  
   　　　　If target[s] <= back_point -> Node-data[s]  
   　　　　　　Kd_point = back_point -> right；  //如果target位于左子空间，就应进入右子空间  
   　　　　else  
   　　　　　　Kd_point = back_point -> left;    //如果target位于右子空间，就应进入左子空间  
   　　　　将Kd_point压入search_path堆栈；  
   　　If Dist（nearest，target） > Dist（Kd_Point -> Node-data，target）  
   　　　　nearest  = Kd_point -> Node-data；                 //更新最近邻点  
   　　　　Min_dist = Dist（Kd_point -> Node-data,target）；  //更新最近邻点与查询点间的距离

当维数较大时，直接利用k-d树快速检索的性能急剧下降。假设数据集的维数为D，一般来说要求数据的规模N满足条件：N远大于2的D次方，才能达到高效的搜索。

SamanthaChen's Blog

统计学习方法（李航）- 第3章k近邻法笔记