决策树在分类问题中表示基于特征对实例进行分类的过程。它可以认为是if then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性，分类速度快。
学习时候，利用训练数据，根据损失函数最小化的原则建立决策树模型，预测时，对新的数据，利用决策树模型进行分类。
决策树学习包括三个步骤：特征选择、决策树的生成和决策树的修剪。

决策树模型与学习

内部节点表示一个特征或者属性，叶节点表示一个类。

决策树与if-then规则

将决策树转换成if-then规则：

• 从决策树的根节点到叶节点的每一条路径构建一条规则
• 路径上内部节点对应规则的条件，叶节点对应结论
  决策树与ifthen集合性质：互斥且完备
  每一个实例都被一条路径或者一条规则覆盖，而且只被一条路径或者一条规则覆盖。

  决策树与条件概率分布

  决策树海表示给定特征条件下的条件概率分布。这一条件概率分布定义在特征空间的一个划分。将特征空间划分为互不相交的单元或者区域，并在每个单元定义一个类的概率分布就构成了一个条件概率分布。决策树的一条路径对应于划分的一个单元。决策树所表示的概率分布由条件下类的条件概率分布组成。

  学习

  决策树本质上式从训练数据中归纳出一组分类规则。与训练数据集不相矛盾的据册数可能有多个，也可能一个也没有。我们需要一个与训练数据集矛盾较小的决策树同时泛化能力好。
  从另一个角度看，决策树学习是由训练数据集估计条件概率模型。基于特征空间划分的类条件概率模型有无穷多个，我们选择的条件概率应该拟合好，预测也好。

决策树损失函数通常是正则化的极大似然函数。当损失函数确定后，选最优决策树是NP完全问题，因此常采用启发算法，近似求解。

决策树的生成对应于模型的局部选择，决策树的修建对应着模型的全局选择

特征选择

选取具有分类能力的特征，可以提高学习效率。
熵只依赖于X的分布，与X的取值无关，熵越大，随机变量不确定性越大。

信息增益

信息增益比

决策树的生成

ID3算法

以信息增益来选择特征，递归构建决策树。

C4.5算法

对ID3进行改进，用信息增益比来选择特征。

决策树的剪枝

$$C_\alpha (T) = C(T)+\alpha|T|$$
第一项是训练误差，第二项是模型复杂度。
可以看出，决策树生成只考虑了提高信息增益对训练数据进行更好的你和，而剪枝过程还考虑了减小模型复杂度。生成学习局部非模型而剪枝学习整体的模型。

CART算法

既可以用于分类也可以用于回归。
两步：

1. 决策树生成，由训练数据生成决策树，树尽量大
2. 用验证数据集对树进行剪枝并选择最优子树，用损失函数最小作为剪枝标准。

CART生成

决策树的生成就是递归的构建二叉决策树的过程。
对回归树用平方误差准则，对分类树用基尼指数最小化准则，进行特征选择。

CART算法采用一种二分递归分割的技术，算法总是将当前样本集分割为两个子样本集，使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。因此CART算法适用于样本特征的取值为是或非的场景，对于连续特征的处理则与C4.5算法相似。

回归树生成

假设X和Y是输入和输出。一个回归树对应着输入空间（特征空间）的一个划分以及在划分的输出值。假设已将输入空间划分为M个单元R1,R2,…,Rm，并且在每个单元有一个固定输出值，回归树模型可以表示为
$$f(x) = \sum_{m=1}^M c_m I(x\in R_m)$$
用平方误差表示回归树的训练误差，平方误差最小准则求解每个单元上的最优输出。单元上cm最优值是Rm上所有输入实例对应的输出均值。对输入空间的划分采用启发式算法，选择（j，s）作为切分变量和切分点，并定义它的左右两个区域，然后在两个区域上找最优切分变量和切分点。
第一步，搜索分裂变量和分裂点，分裂点(j,s)

搜索的分离变量j和分裂点s的目标函数;

这样的回归树通常称作最小二乘回归树。

分类树的生成

分类树选择基尼指数做特征选择，同时决定该特征的最优二分切分点。

数据集D的纯度可以用基尼值来衡量：
$$Gini(D) = \sum_{k=1}^{|\mathcal{Y}|} \sum_{k’ \neq k} p_k p_{k’} = 1- \sum_{k=1}^{|\mathcal{Y}|} p_k^2$$
直观地说，Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，因此Gini越小则数据D的纯度越高。
属性a的基尼指数定义为：
$$Gini_index(D,a) = \sum_{v=1}^V \frac{|D^v|}{|D|}Gini(D^v)$$
于是我们在候选属性集A中，选择哪个使得划分后基尼指数最小的属性作为最优划分属性，即$a_* = argmin_{a\in A} (Gini_index(D,q))$

Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A = a分割后D的不确定性，Gini越大，不确定性越大，与熵相似。

基尼指数，熵之半和分类误差率曲线都和接近，都可以近似代表分类误差。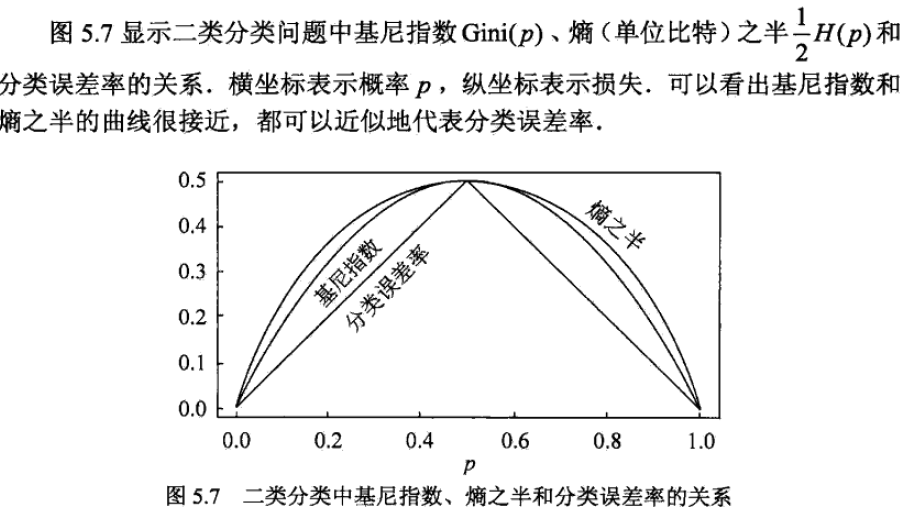

CART剪枝

剪枝过程特别重要，所以在最优决策树生成过程中占有重要地位。有研究表明，剪枝过程的重要性要比树生成过程更为重要，对于不同的划分标准生成的最大树(Maximum Tree)，在剪枝之后都能够保留最重要的属性划分，差别不大。反而是剪枝方法对于最优树的生成更为关键。

CART剪枝算法从“完全生长”的决策树底端剪去一些子树，使得模型边检大，从而能够对未知数据有更准确的预测。

算法分成两个步骤：首先从生成算法产生的决策树底端T0开始不断剪枝，知道T0根节点，形成一个子树序列{T0，T1，…,Tn}；然后通过交叉验证法在独立的验证数据集上对子树进行测试，从中选择最优子树。

损失函数：
$$C_\alpha (T) = C(T)+\alpha|T|$$
对于固定的$\alpha$，一定存在唯一的使得损失函数最小的最优子树。$\alpha$大，最优子树偏小，反之，$\alpha$小，最优子树偏大。
已经有证明可以用递归的方法对树进行剪枝。

具体的，从整体树T0开始剪枝，对T0内任意内部节点t，以t为单节点的损失函数是
$$C_\alpha (t) = C(T)+\alpha$$
以t为根的子树Tt损失函数是
$$C_\alpha (T_t) = C(T_t)+\alpha|T_t|$$
（|T_t|难道<1?）
当 alpha = 0或者充分小的时候,有
$$C_\alpha (T_t) < C_\alpha (t)$$
alpha 仔增发，只要$\alpha = \frac{C(t)-C(T_t)}{|T_t|-1}$，Tt与t有相同损失函数，而t的节点更少，因此t比Tt更可取，对Tt进行剪枝。
因此对T0中每个内部节点t计算
$$g(t) = \frac{C(t)-C(T_t)}{|T_t|-1}$$
表示剪枝后整体损失函数减少的程度。