软间隔与正则化

在前面袈裟中我们一直假设训练样本在样本空间或者特征空间中是线性可分的，即存在一个超平面能将不同类的样本完全划分开。

• 然而现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；
• 即时找到了某个核函数使得训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果是不是过拟合所造成的。
  例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。例如下图：
  
  用黑圈圈起来的那个蓝点是一个 outlier ，它偏离了自己原本所应该在的那个半空间，如果直接忽略掉它的话，原来的分隔超平面还是挺好的，但是由于这个 outlier 的出现，导致分隔超平面不得不被挤歪了，变成途中黑色虚线所示（这只是一个示意图，并没有严格计算精确坐标），同时 margin 也相应变小了。当然，更严重的情况是，如果这个 outlier 再往右上移动一些距离的话，我们将无法构造出能将数据分开的超平面来。

缓解该问题的一个办法就是引入”软间隔（soft margin）”。具体来说，前面介绍的支持向量机是要求所有样本均满足约束，即所有的而样本均划分正确，称为“硬间隔”，而软间隔就是允许某些样本不满足约束:

$$y_i(w^Tx_i+b)\geq 1, \quad i=1,\ldots,n \quad (1)$$

当然，在最大化间隔的同时，不满足约束的样本应该尽可能少，于是优化目标可以写成：

$$\min_{w,b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^m \mathcal{l}_{0/1}(y_i (w^T x_i +b ) -1) \quad (2)$$

其中 C>0 是一个常数，$\mathcal{l}_{0/1}$ 是“0/1损失常数”

$$\mathcal{l}_{0/1} =
\begin{cases}
1 & if \quad z<0 \\
0 & otherwise
\end{cases} \quad (3)$$

显然，当C为无穷大的时候，式子（2）迫使所有样本满足式子（1），于是等价于SVM基本型；当C取有限值的时候，式子(2)允许一些样本不满足约束。

然而，$l_{0/1}$ 非凸、非连续，使得(2)不易直接求解。于是我们通常采用其他一些函数来代替，称为“替代损失”。替代损失函数一般具有较好的数学性质，如他们通常是凸的联系函数并且是 $l_{0/1}$ 的上界。，如图给克三种常用的替代损失函数：

• hinge 损失：$l_{hinge}(z) = max(0, 1-z) $
• 指数损失：$l_{exp}(z) = \exp(-z) $
• 对率损失：$l_{log}(z) = \log(0, \exp(-z) $ （是对率函数的变形 log 可用ln）
  若采用hinge损失：

$$\min_{w,b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^m \max (0,1-y_i (w^T x_i +b )) \quad (2)$$

引入松弛变量ξi≥0 ,对应数据点 xi 允许偏离的 functional margin 的量。当然，如果我们运行 ξi 任意大的话，那任意的超平面都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些 ξi 的总和也要最小：:

$$\begin{align}
\min & \frac{1}{2}|w|^2 + C\sum_{i=1}^n\xi_i \
s.t., & y_i(w^Tx_i+b)\geq 1-\xi_i, i=1,\ldots,n \
& \xi_i \geq 0, i=1,\ldots,n
\end{align}$$

其中 C 是一个参数，用于控制目标函数中两项（“寻找 margin 最大的超平面”和“保证数据点偏差量最小”）之间的权重。注意，其中 ξ 是需要优化的变量（之一），而 C 是一个事先确定好的常量。
这就是常用的“软间隔支持向量机”.

显然，每个样本都有一个对应的松弛变量，泳衣表征该样本不满足约束的程度，但是，解决这个问题仍是个二次规划问题，于是通过与上一节类似的拉格朗日乘子法可以得到：

$$\mathcal{L}(w,b,\xi,\alpha,r)=\frac{1}{2}|w|^2 + C\sum_{i=1}^n\xi_i – \sum_{i=1}^n\alpha_i \left(y_i(w^Tx_i+b)-1+\xi_i\right) – \sum_{i=1}^n r_i\xi_i$$

分析方法和前面一样，转换为另一个问题之后，我们先让 L 针对 w、b 和 ξ 最小化：

$$\begin{align}
\frac{\partial \mathcal{L}}{\partial w}=0 &\Rightarrow w=\sum_{i=1}^n \alpha_i y_i x_i \
\frac{\partial \mathcal{L}}{\partial b} = 0 &\Rightarrow \sum_{i=1}^n \alpha_i y_i = 0 \
\frac{\partial \mathcal{L}}{\partial \xi_i} = 0 &\Rightarrow C-\alpha_i-r_i=0, \quad i=1,\ldots,n
\end{align} $$

将 w 带回 L 并化简，得到和原来一样的目标函数：

$$\max_\alpha \sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle$$

不过，由于我们得到 C−αi−ri=0 ，而又有 ri≥0 （作为 Lagrange multiplier 的条件），因此有 αi≤C ，所以整个 dual 问题现在写作：

$$\begin{align}
\max_\alpha &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle \
s.t., &0\leq \alpha_i\leq C, i=1,\ldots,n \
&\sum_{i=1}^n\alpha_iy_i = 0
\end{align}$$

和之前的结果对比一下，可以看到唯一的区别就是现在 dual variable α 多了一个上限 C 。而 Kernel 化的非线性形式也是一样的，只要把 换成 κ(xi,xj) 即可。这样一来，一个完整的，可以处理线性和非线性并能容忍噪音和 outliers 的支持向量机才终于介绍完毕了。 :)

替代损失函数问题

有一点需要注意：

通过求解替代函数损失函数得到的是否仍是原来问题的解？这理论称为替代损失的“一致性”问题，有论文给出了一致性的充要条件。

对率回归（逻辑回归）和SVM区别：

可以发现，若果用对率损失函数$l_{log}$替代0/1损失（不是合页损失吗？）函数，则几乎就得到了对率回归模型。

• 实际上支持向量机和对率回归的优化目标相近，通常情况下他们的性能相当。
• 对率回归的优势主要对于其输出具有自然的概率意义，即在给出预测标记的同时也给了概率，而支持向量机的输出不具有概率意义，欲得到概率需要进行特殊处理；
• 此外，对率回归能够直接用于多分类任务，支持向量机为此需要进行推广。
• 另一方面，可以看出hinge损失函数有一块平摊的零区域，这使得支持向量机的解具有稀疏性，而对率损失是光滑的而单调递减函数，不能导出类似支持向量的概念。因此对率回归的解依赖于更多的训练样本，其预测开销大。

他人的解答

来源

我们先来看一下带松弛变量的 SVM 和正则化的逻辑回归它们的损失函数：

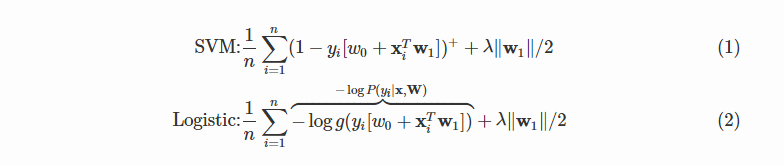
其中 $g(z)=(1+\exp(-z))^{-1}$
可以将两者统一起来: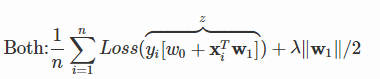

也就是说，它们的区别就在于逻辑回归采用的是 log loss（对数损失函数），svm采用的是hinge loss →E(z)=max(0,1−z)→E(z)=max(0,1−z)。

SVM 损失函数 : Loss(z)=(1−z)+Loss(z)=(1−z)+
LR 损失函数: Loss(z)=log(1+exp(−z))

这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重,两者的根本目的都是一样的。

svm考虑局部（支持向量），而logistic回归考虑全局，就像大学里的辅导员和教师间的区别

辅导员关心的是挂科边缘的人，常常找他们谈话，告诫他们一定得好好学习，不要浪费大好青春，挂科了会拿不到毕业证、学位证等等，相反，对于那些相对优秀或者良好的学生，他们却很少去问，因为辅导员相信他们一定会按部就班的做好分内的事；而大学里的教师却不是这样的，他们关心的是班里的整体情况，大家是不是基本都理解了，平均分怎么样，至于某个人的分数是59还是61，他们倒不是很在意。

另一个总结

1、LR采用log损失，SVM采用合页损失。
2、LR对异常值敏感，SVM对异常值不敏感。
3、在训练集较小时，SVM较适用，而LR需要较多的样本。
4、LR模型找到的那个超平面，是尽量让所有点都远离他，而SVM寻找的那个超平面，是只让最靠近中间分割线的那些点尽量远离，即只用到那些支持向量的样本。
5、对非线性问题的处理方式不同，LR主要靠特征构造，必须组合交叉特征，特征离散化。SVM也可以这样，还可以通过kernel。
6、svm 更多的属于非参数模型，而logistic regression 是参数模型，本质不同。其区别就可以参考参数模型和非参模型的区别

什么时候用SVM，LR？

来自 Andrew NG：

1. 如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM
2. 如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel
3. 如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况
   仔细想想，为什么是这样？
   (LR和不带核函数的SVM比较类似。)

其他损失函数

我们还可以把0/1损失函数换成别的损失函数得到其他学习模型，这些模型性质与其所用的替代函数直接相关，但他们具有一个共性：优化目标的第一项用来秒速划分超平面的“间隔”大小，另一项用来表述训练集上的误差，可以写成更一般的形式:

$$\min_f \Omega (f) + C \sum_{i=1}^m \mathcal{l} (f(x_i),y_i)$$

• 其中 $\Omega (f)$ 称为“结构风险”，用于描述模型f的某些性质；
• 第二项称为“经验风险”，用于描述模型与训练数据的契合程度；
• C用于对二者折中。

从经验风险最小化角度看，

• $\Omega (f)$表述了我们希望获取哪种性质的模型（例如希望获得复杂度比较小的模型），这为引入领域知识和用户意图提供了途径；
• 另一方面，该信息有助于消减假设空间，降低了最小化训练误差的过拟合风险。

从这个角度说，上面的式子成为“正则化问题”，$\Omega (f)$称为正则化项，C称为正则化常数。Lp范数是常用的正则化项，其中L2范数||w||2倾向于 $mathbf{w}$ 的分量取值尽量平衡,即非零个数尽量稠密，而L0范数和L1范数则倾向于w的分量尽量稀疏，即非0个数尽量少。

“正则化问题”可以理解为一种“罚函数法”，即对不希望得到的结果加以惩罚，从而使优化过程趋向于希望目标。从贝叶斯估计的角度看，正则化项可认为是提供了模型的先验概率。

支持向量回归（Support Vector Regression，SVR）

核方法

给定训练样本，若不考虑偏移量b，则无论SVM还是SVR，学得的模型总能表示成核函数的组合。我们还有定理证明核函数对损失函数没有限制，对正则化$\Omega$ 仅要求单调递增，甚至不要求是凸函数，意味着对一般的损失函数和正则化项，优化问题的最优解都可以表示成核函数的线性组合，这显示出核函数的巨大威力。

人们发展出一系列基于核函数的学习方法，统称“核方法”。最常见的通过“核化（即引入核函数）”来讲线性学习器拓展为非线性学习器，从而得到“核线性判别分析”（KLDA）。

其他关于SVM的问题

1. 高斯核SVM和RBF神经网络的区别
   若将隐层神经元数目设置为训练样本数，且每个训练样本对应一个神经元中心，则以高斯径向基函数为激活函数的RBF网络恰好与高斯核SVM预测函数相同。