统计学习方法(李航)- 第10章隐马尔科夫模型笔记
隐马尔科夫模型是可用于标注问题的统计学习模型,描述由隐藏的马尔科夫随机链生成观测序列的过程,属于生成模型。
定义
隐马尔科夫模型是关于时序的概率模型,描述一个隐藏的马尔科夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔科夫随机生成的状态的序列,称为状态序列;每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列,序列的每一个位置又可以看做是一个时刻。
隐马尔科夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。
形式定义如下:
设Q是所有可能的状态集合,V是所有可能的观测集合,其中N是状态数,M是可能的观测数。I是长度为T的状态序列,O是对应的观测序列。A是N*N的状态转移矩阵,是t时刻处于状态i在t+1转移带q的概率。B是N*M的观测概率矩阵。π是初始状态概率向量。
隐马尔科夫模型由初始状态π、状态转移概率矩阵A和观测矩阵B决定。π和A决定状态序列,B决定观测序列,因此隐马尔科夫模型可以用三元符号表示:
λ = (A, B, π)
A, B, π 称为隐马尔科夫模型的三要素。
隐马尔科夫模型做了两个基本假设:
- 齐次马尔科夫假设,即假设隐藏的马尔科夫链在任意t时刻状态只依赖于前一时刻状态,与其他时刻的状态以及观测无关,夜雨时间t无关。
- 观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测以及状态无关。
观测序列的生成
- 按照初始状态分布 π 产生状态i
- 按照状态i_t的观测概率生成观测序列O_t
- 按照状态i_t的转移概率分布生成状态i_t+1
- 若 t < T,令 t = t + 1,并且转移到算法第2步继续执行,否则结束。
隐马尔科夫模型的三个基本问题
概率计算问题。给定模型λ = (A,B,π)和观测序列O=(o1, o2, …, oT),计算在模型λ下观测序列出现的概率P(O|λ)
预测\解码问题。给定模型λ = (A,B,π)和观测序列O=(o1, o2, …, oT),求对给定的关系序列条件概率P(I|O)最大的状态序列I=(i1, i2, …,iT)。即给定观测序列,求最有可能的对应的状态序列。
学习问题。已知观测序列O=(o1, o2, …, oT),估计模型λ = (A,B,π)参数,使得在该模型下观测序列概率P(O|λ)最大。即用极大似然的方法估计参数。
问题1:概率估算问题
概率计算算法
理论上,可以通过穷举所有状态转换序列的办法计算观察序列O的概率。
实际上,这样做并不现实。
直接计P(O|λ)计算量是O(TN^T)阶的。
前向算法
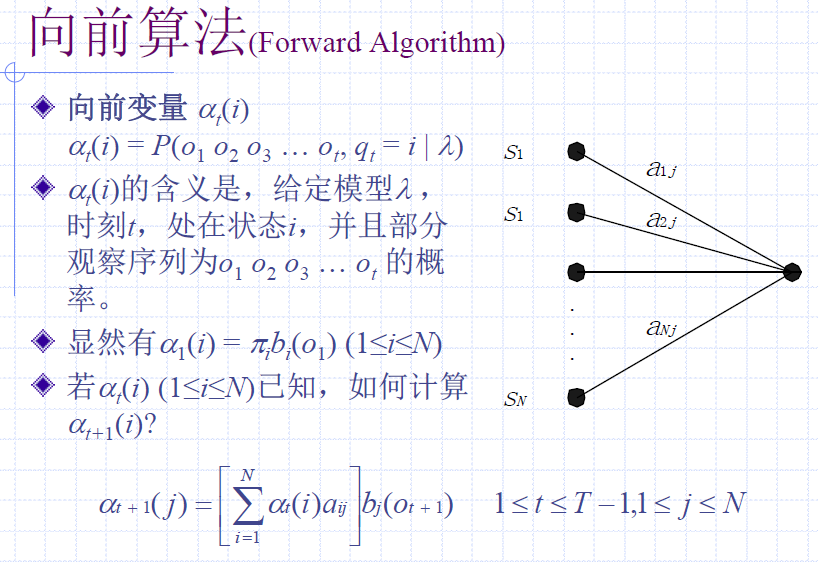

后向算法

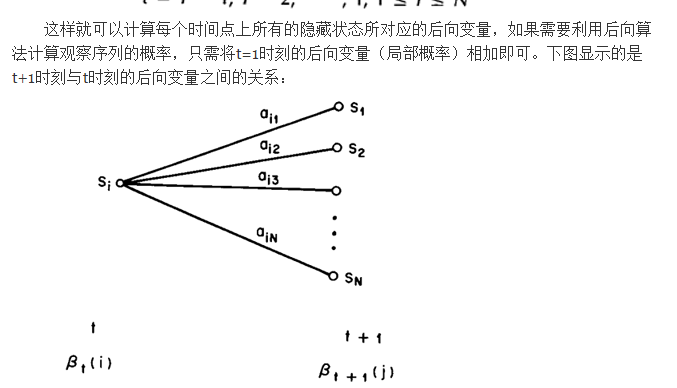

一些概率和期望值的算法
- t时刻处于状态qi的概率可以可利用t时刻前向概率和后向概率计算。
- t时刻处于状态qi, j时刻处于qi+1的概率可以可利用t时刻前向概率、转移概率、输出概率和t+1的后向概率计算。
- 可以利用1的单个状态和2的两个状态计算一些期望



问题2:预测问题
一般有两种解法,近似算法和维特比算法
近似算法
思想是在每个时刻t选择该时刻最有可能出现的状态,将它作为一个预测结果。
利用前面的前向概率和后向概率计算t时刻处于i的状态的概率,然后从这些状态里面选择概率最大的。这些每个时刻最大的状态合起来就构成了状态序列。
计算算法的优点是计算简单,缺点是不能保证预测的状态序列整体上是最有可能的状态序列,因为预测的状态序列可能有实际不发生的部分。
事实上上述方法得到的状态序列中可能存在转移概率为0的相邻状态。尽管如此近似算法还是有用的(??个人存疑)
维特比算法
维特比算法实际上式用动态规划求解隐马尔科夫模型预测问题,即用动态规划求概率最大的路径,这时一条路径对应着一个状态序列。
根据动态规划原理,最优路径应该存在这样特性:最优路径的子路径也一定是最优的。
动态规划的转移方程:
dp[t+1] = max(dp[t]x状态转移概率)x输出概率
其中dp[t]表示t时刻最佳状态转移序列的概率。因此还需要一个数组保存状态转移的路径,最后要对最优路径进行回溯。


问题3: 学习问题
根据训练数据是包括观测序列和对应的状态,还是只有观测序列,可以分别由监督学习和无监督学习实现。
监督学习方法
假定已经给出多个观测序列和对应的状态序列,可以利用极大似然法来估计参数。

参数学习十分简单,在训练数据足够强大的前提下,效果不错。
缺点:状态信息未知的时候无法使用,或者需要人工标注状态,代价高。
但是在无监督学习效果不佳的时候可以采用有监督学习。
非监督学习
假设给定的训练数据只包含s个长度为T的观测序列,而没有对应的状态序列,目标是学习隐马尔科夫模型的参数。我们将观测序列数据看做观测状态O,状态序列数据看做不可观测的隐数据I,那么马尔科夫模型实际上是一个含有隐变量的概率模型。它的参数学习可以由EM算法实现。
Baum-Welch算法





Baum等人证明要么估算参数值和估算前的参数值相等,要么估算值比估算前的参数值更好的解释了观察序列O。
参数最终的收敛点并不一定是一个全局最优值,但一定是一个局部最优值。(在函数非凸时候可能获得局部最优?)
L.R.Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech recognition, Proc. IEEE, 77(2): 257-286, 1989

